在物理学和材料科学的广阔领域中，对称性扮演着至关重要的角色，它不仅是理解宇宙基本定律的基石，也是设计和发现新材料功能的基础。然而，与对称性同样引人入胜的，是不对称性——特别是手性和轴性——它们在自然界中无处不在，从生物分子的镜像异构体到复杂晶体结构中展现出的独特宏观性质。

长期以来，对手性和轴性的定量描述主要集中在原子排列的结构不对称性上。然而，一篇发表在PRL题为“Quantification of Electronic Asymmetry: Chirality and Axiality in Solids”的开创性论文，突破了这一传统视角，将焦点转向了更为微观和本质的电子不对称性，为固态材料中手性和轴性的量化提供了一个全新的、基于电子手性分布的框架。

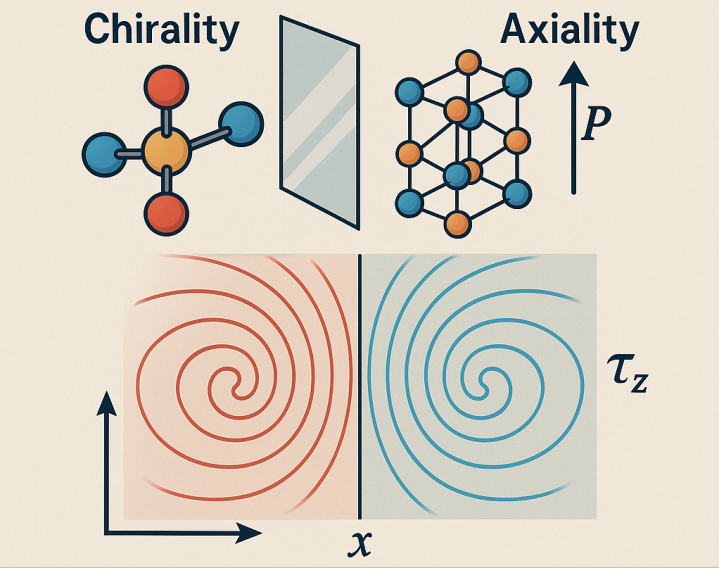
手性，简单来说，是指一个物体不能通过任何旋转或平移与它的镜像重合的性质，就像我们的左手和右手。在材料科学中，手性材料因其独特的光学、电学和磁学性质而备受关注，例如圆偏振光吸收的圆二色性效应以及手性诱导自旋选择性效应。轴性则与极性相关，但允许垂直于主轴的镜面对称，通常表现出沿某一方向的各向异性响应。尽管这些不对称性现象引人入胜并具有巨大的应用潜力，但对其进行严格和普适的量化一直是一个挑战。传统的量化方法往往依赖于原子位置的几何定义，但这通常不够唯一和普适，尤其难以捕捉到电子层面上的精妙不对称性。

正是为了解决这一难题，这篇论文提出了一种范式转换。它摒弃了仅仅关注原子核位置的结构层面，转而深入探究电子本身固有的不对称性——电子手性。在相对论量子理论中，电子手性作为狄拉克场的一个基本自由度，与电子的电荷和自旋同等重要。研究人员认为，尽管凝聚态物理中通常更关注电子的电荷和自旋自由度，但电子手性作为一个在时间反演下保持不变，同时局部破坏反演对称性和镜面对称性的量，正是描述材料手性程度的理想微观量。

该论文的核心贡献在于提出了基于电子手性分布的定量指标。它定义了材料的总手性为电子手性分布 τZ(r) 在空间中的积分，C=∫dr⟨τZ(r)⟩。这一量在空间反演操作下具有奇对称性，这意味着如果材料具有手性，则其手性值在空间反演后会改变符号。与手性类似，论文进一步定义了轴性，将其量化为电子手性分布的极化，表示为 X=∫dr(rτZ(r))。有趣的是，轴性在空间反演下具有偶对称性。这种定义方式，如同通过电荷分布判断材料是否具有极性一样，使得人们可以从电子手性分布中直观地判断材料是否具有手性或轴性。这些量不再是模糊的定性描述，而是具有明确物理意义的微观定量指标。

为了验证这些新提出的量化指标的有效性，研究人员采用了第一性原理计算。通过这些高精度的计算，他们能够模拟和评估材料中电子手性分布的精确空间特性，并将其与自旋诱导的电极化等其他物理量进行关联。这种扎实的理论验证，为电子不对称性的新量化框架提供了坚实的科学基础，证明了其在描述不对称材料方面的普适性和准确性。

更为重要的是，论文还提出了一个具有重大实践意义的实验观测途径：光电子能谱中的圆二色性。圆二色性是一种测量材料对左旋和右旋圆偏振光吸收差异的技术，长期以来被用于研究手性分子的结构。该论文指出，通过光电子能谱中的圆二色性，可以直接观测到电子手性，从而将理论预测与实验测量紧密联系起来。这一提议为实验物理学家提供了一个直接探测和量化电子不对称性的方法，有望加速新型手性和轴性材料的发现和表征。

这篇论文的影响是深远的。它不仅提供了一个严谨的理论框架来量化固体中的手性和轴性，而且通过将焦点从结构不对称性转移到电子手性这一基本量子性质，为我们理解和探索不对称材料开辟了新的天地。例如，在非磁性材料中，电子手性可能扮演着关键角色，其在过去由于主要关注自旋而可能被忽视。此外，这一新框架将极大地促进具有定制化不对称性质的新型功能材料的设计和发现，例如在自旋电子学、拓扑材料、以及能量转换和催化等领域。通过将电子手性、轴性和自旋诱导的电极化结合起来，该研究为不对称材料提供了一个统一而强大的描述语言，为探索诸如手性诱导自旋选择性等复杂交叉耦合现象提供了更深层次的见解。